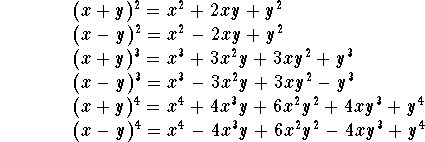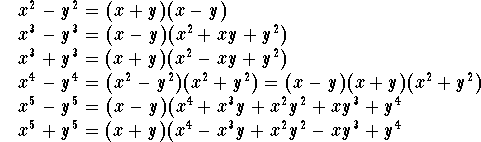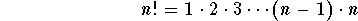Algebra

बीजगणित चर और संख्या के साथ संबंधित है।

बीजगणित बुनियादी गणित है, यह एक दूसरे के साथ दो या दो से अधिक चर और संख्या से संबंधित है जो सूत्रों की बड़ी संख्या के साथ संबंधित है।

यहाँ आप मदद बीजीय फार्मूले की एक सूची है।

बेसिक बीजीय सूत्र:

दो और तीन चर के बीच बुनियादी संबंध से जुड़े बीजीय फार्मूले हैं:

1>

$a^2-b^2 = (a+b)\times (a-b)$

2>

$a^2+b^2 = (a+b)^2-2ab=(a-b)^2+2ab$

3>

$(a+b)^2 = a^2+2ab+b^2 = (a-b)^2+4ab$

4>

$(a-b)^2 = a^2-2ab+b^2 = (a+b)^2-4ab$

5>

$a^3+b^3 = (a+b) \times (a^2-ab+b^2) = (a+b)^3-3ab \times (a+b)$

6>

$a^3-b^3 = (a-b) \times (a^2+ab+b^2) = (a-b)^3+3ab \times (a-b)$

7>

$(a+b)^3 = a^3+3a^2b+3ab^2+b^3 = a^3+b^3+3ab \times (a+b)$

8>

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3 = a^3-b^3-3ab \times (a+b)$

9>

$(x+a) \times (x+b) = x^2+x \times (a+b)+ab$

10>

$(x-a) \times (x+b) = x^2+x \times (b-a)-ab$

11>

$(x-a) \times (x-b) = x^2-x \times (a+b)+ab$

12>

$(a+b+c)^2 = a^2+b^2+c^2+2ab+2bc+2ac$

13>

$(a+b+c)^3 = a^3+b^3+c^3+3(a+b)(b+c)(c+a)$

14>

$a^4-b^4 = (a-b) \times (a+b) \times (a^2+b^2)$

15>

$a^6-b^6 = (a+b) \times (a^2-ab+b^2) \times (a-b) \times (a^2+ab+b^2)$

16>

$a^6+b^6 = (a^2+b^2) \times (a^4-a^2b^2+b^4)$

17>

$a^4+a^2b^2+b^4 = (a^2-ab+b^2) \times (a^2+ab+b^2)$

18>

$(a-b-c)^2 = a^2+b^2+c^2-2ab+2bc-2ac$

19>

$a^3+b^3+c^3-3abc = (a+b+c) \times (a^2+b^2+c^2-ab-bc-ac)$

सूचकांकों सूत्र:

चर और उनकी शक्तियों या शक्तियों और सूचकांक के बीच संबंधों से जुड़े सूत्र हैं:

1>

$x^m \times x^n = x^{m+n}$
और
$x^m \times x^n \times \ldots \times x^p = x^{m+n+ \ldots +p}$

2>

$x^m \div x^n = x^{m-n}$
और
$x^m \div x^n \div \ldots \div x^p = x^{m-n- \ldots -p}$

3>

$(x^m)^n = x^{m \times n}$
और
$((x^m)^n)^o) = x^{m \times n \times o}$

4>

$x^0 = 1$

5>

$x^{-m} = \dfrac{1}{x^m}$
और
$x^{m} = \dfrac{1}{x^{-m}}$

6>

$x^{\frac{m}{n}} = \sqrt[n]{x^m}$

7>

$\left( \dfrac{x^a}{y^b} \right)^c = \dfrac{x^{ac}}{y^{bc}}$

8>

$\dfrac{x^m}{y^m} = \left( \dfrac{x}{y} \right)^m$

9>

$\sqrt[m]{\dfrac{x^a}{y^b}} = \dfrac{x^{\frac{a}{m}}}{y^{\frac{b}{m}}}$

10>

$x^{\frac{p}{q}} = \sqrt[q]{x^p} = \left(\sqrt[q]{x}\right)^p$

11>
$\sqrt[m]{\dfrac{x}{y}} = \dfrac{\sqrt[m]{x}}{\sqrt[m]{y}}$

12>

$\sqrt{a} \times \sqrt {b} = \sqrt{a \times b}$ ए, बी और एक ख * नकारात्मक संख्या नहीं कर रहे हैं प्रदान की है।

13>

, तो $a^x = a^y$ तो, y = x। ( उसे उपलब्ध कराया : $0 < a\text{ and }a \ne 1$ )

14>

, तो $a^x = b^x$ तो, एक = बी। ( उसे उपलब्ध कराया : $0 < a , b \text{ and }a , b \ne 1$ )

displaymath99 displaymath113

displaymath107

This website was created for free with Own-Free-Website.com. Would you also like to have your own website?

Sign up for free